第一题:如图,已知\(A\)、\(B\)、\(C\)为\(\odot O\)上三点,\(\angle AOC = 150^{\circ}\),则\(\angle ABC = \)( )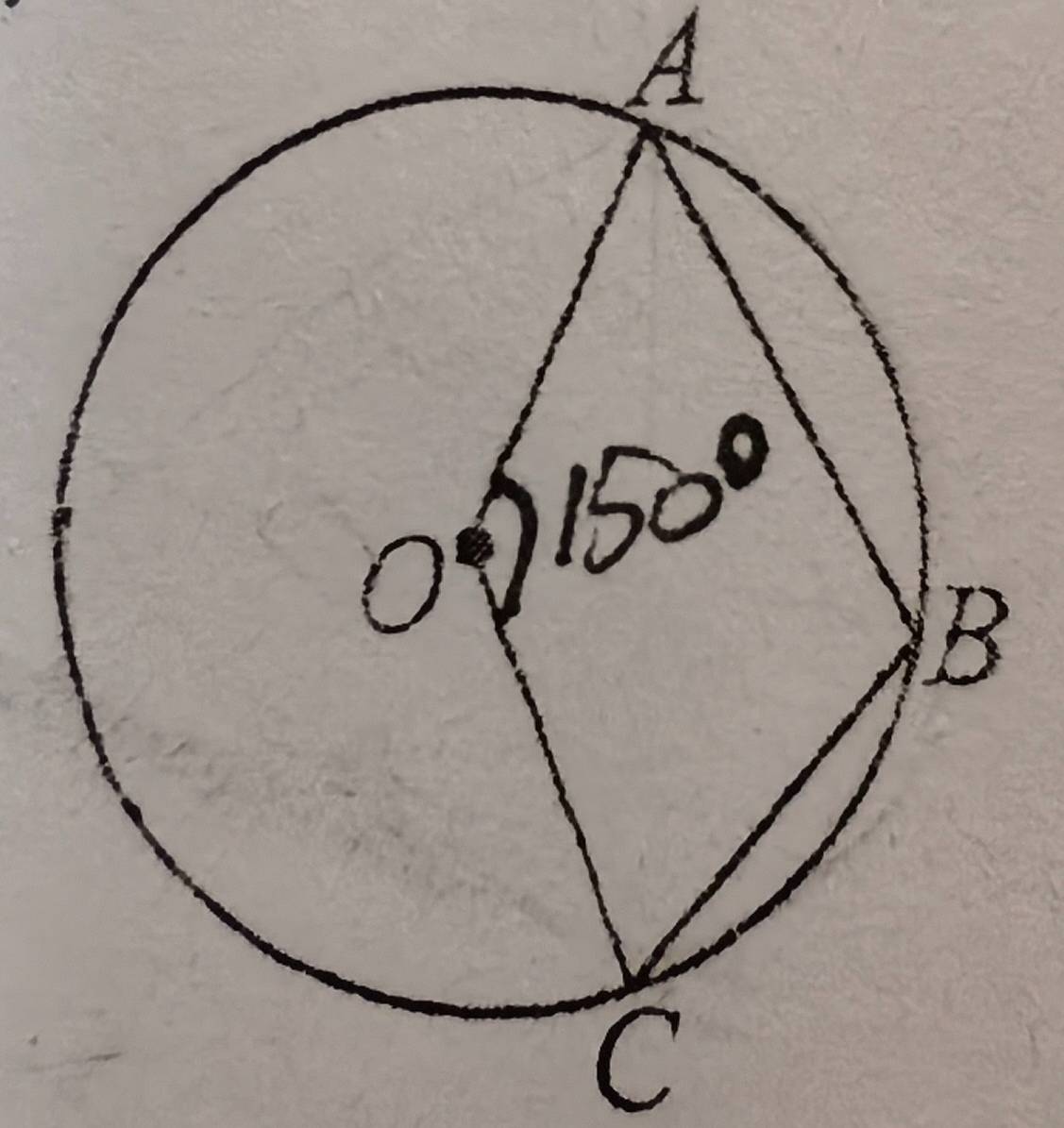
A. \(105^{\circ}\)
B. \(120^{\circ}\)
C. \(135^{\circ}\)
D. \(150^{\circ}\)
本题涉及圆周角定理:同弧或等弧所对的圆周角等于圆心角的一半,即若圆心角为\(\angle AOC\),圆周角为\(\angle ABC\)(同弧\(\overset{\frown}{AC}\)),则\(\angle ABC = \dfrac{1}{2}\angle AOC\)(这里需注意弧对应的情况,本题要先处理优弧 )。
求优弧\(\boldsymbol{\overset{\frown}{AC}}\)所对的圆心角:
已知\(\angle AOC = 150^{\circ}\),整个圆周角为\(360^{\circ}\),设优弧\(\overset{\frown}{AC}\)所对圆心角为\(\angle AOC'\),则\(\angle AOC' = 360^{\circ} - 150^{\circ}\),即\(\angle AOC' = 210^{\circ}\) 。
根据圆周角定理求\(\boldsymbol{\angle ABC}\):
因为\(\angle ABC\)是优弧\(\overset{\frown}{AC}\)所对的圆周角,\(\angle AOC'\)是优弧\(\overset{\frown}{AC}\)所对的圆心角,由圆周角定理可知\(\angle ABC = \dfrac{1}{2}\angle AOC'\) 。
把\(\angle AOC' = 210^{\circ}\)代入,可得\(\angle ABC = \dfrac{1}{2} \times 210^{\circ} = 105^{\circ}\) ,用 KaTeX 表示:\(\angle ABC = \dfrac{1}{2} \times 210^{\circ} = 105^{\circ}\) 。
综上,\(\angle ABC\)的度数为\(105^{\circ}\),答案选\(\boldsymbol{A}\)选项。
第二题:已知\(A\)、\(B\)、\(C\)为\(\odot O\)上三点,\(\angle AOB = 60^{\circ}\),则\(\angle ACB = \)____。
本题答案是\(\boldsymbol{30^{\circ}}\)或\(\boldsymbol{150^{\circ}}\) ,原因在于点\(C\)的位置存在两种情况:
情况一:点\(C\)在优弧\(\boldsymbol{\overset{\frown}{AB}}\)上
根据圆周角定理:同弧或等弧所对的圆周角等于圆心角的一半 。\(\angle AOB\)是圆心角,\(\angle ACB\)是圆周角,它们都对着弧\(\overset{\frown}{AB}\),所以\(\angle ACB = \frac{1}{2}\angle AOB\) 。
已知\(\angle AOB = 60^{\circ}\),则\(\angle ACB = \frac{1}{2}\times 60^{\circ}= 30^{\circ}\) 。
情况二:点\(C\)在劣弧\(\boldsymbol{\overset{\frown}{AB}}\)上
圆内接四边形对角互补,构造圆内接四边形\(AC'BC\)(\(C'\)是优弧\(\overset{\frown}{AB}\)上一点 ),那么\(\angle ACB + \angle AC'B = 180^{\circ}\) 。
因为前面已求出优弧\(\overset{\frown}{AB}\)所对的圆周角\(\angle AC'B = 30^{\circ}\),所以劣弧\(\overset{\frown}{AB}\)所对的圆周角\(\angle ACB = 180^{\circ} - 30^{\circ}= 150^{\circ}\) 。
综上,由于点\(C\)在圆上的位置有在优弧和劣弧两种可能,所以\(\angle ACB\)有两个答案,分别是\(\boldsymbol{30^{\circ}}\)和\(\boldsymbol{150^{\circ}}\)。