本题可通过作弦心距，利用垂径定理求出弦长的一半，再结合勾股定理求出弦心距，然后根据全等三角形的性质求出相关角度，最后在直角三角形中利用三角函数求出OM的长。
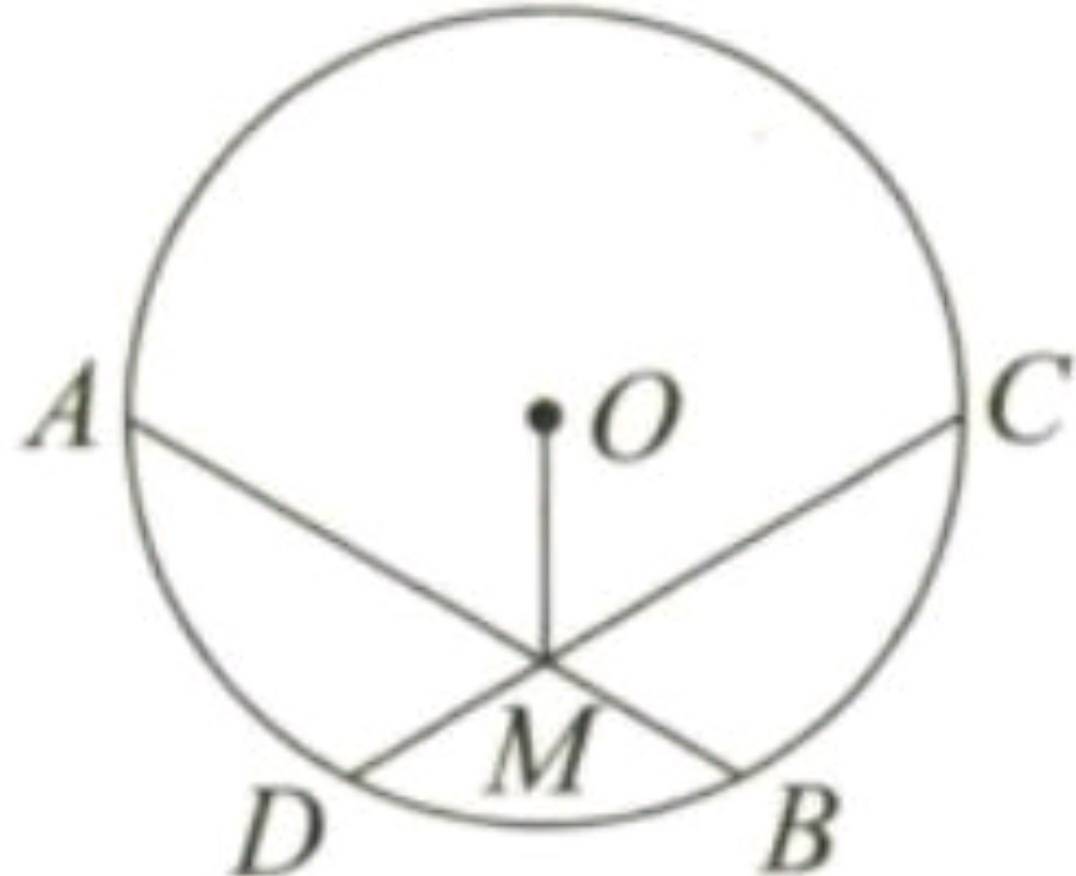
如图，在半径为 2 的\(\odot O\)中，弦\(AB\)与弦\(CD\)相交于点\(M\)，如果\(AB = CD = 2\sqrt{3}\)，\(\angle AMC = 120^{\circ}\)，求\(OM\)的长 。
勾股定理运算错误。
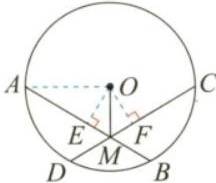作辅助线：过点\(O\)作\(OE\perp AB\)于\(E\)，\(OF\perp CD\)于\(F\)，连接\(OA\)。
根据垂径定理，垂直于弦的直径平分弦，所以\(AE = \frac{1}{2}AB\)，\(CF = \frac{1}{2}CD\)。
因为\(AB = CD = 2\sqrt{3}\)，则\(AE = \frac{1}{2}\times 2\sqrt{3}=\sqrt{3}\) 。
在\(Rt\triangle AOE\)中，\(OA = 2\)（圆半径），\(AE = \sqrt{3}\)，由勾股定理\(OE = \sqrt{OA^{2}-AE^{2}}\)，即：
\(OE = \sqrt{2^{2}-\left(\sqrt{3}\right)^{2}}=\sqrt{4 - 3}= 1\) 。
因为\(AB = CD\)，所以弦心距\(OE = OF\)，又\(OM\)为公共边，\(\angle OEM = \angle OFM = 90^{\circ}\)，可得\(Rt\triangle OEM\cong Rt\triangle OFM\)（HL 定理） 。
所以\(\angle OME = \frac{1}{2}\angle AMC\)，已知\(\angle AMC = 120^{\circ}\)，则\(\angle OME = 60^{\circ}\) 。
在\(Rt\triangle OEM\)中，\(\sin\angle OME = \frac{OE}{OM}\)，即\(\sin60^{\circ}=\frac{1}{OM}\) 。
因为\(\sin60^{\circ}=\frac{\sqrt{3}}{2}\)，所以\(OM = \frac{1}{\sin60^{\circ}}=\frac{2\sqrt{3}}{3}\) 。