本题涉及圆的性质以及圆心角与弦的关系。通过构造辅助角，利用全等三角形的性质来求解弦 AB 的长。
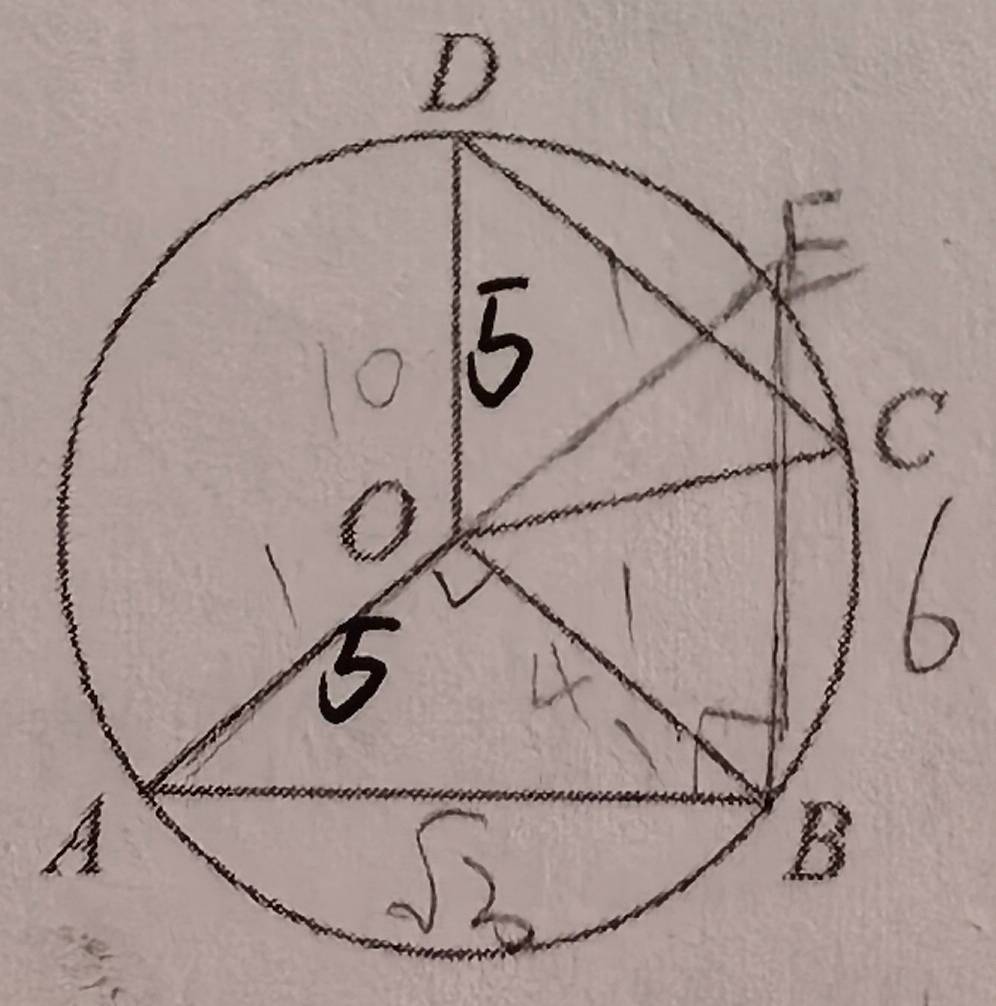如图，已知\(\odot O\)的半径为\(5\)，弦\(AB\)，\(CD\)所对的圆心角分别是\(\angle AOB\)，\(\angle COD\)，若\(\angle AOB\)与\(\angle COD\)互补，弦\(CD = 6\)，则弦\(AB\)的长为（ ）。
A. \(6\)
B. \(8\)
C. \(5\sqrt{2}\)
D. \(5\sqrt{3}\)
构造辅助线没在图上画出，导致题目做不出来。
构造辅助线与角度关系推导
延长\(AO\)交\(\odot O\)于\(E\)，则\(AE\)为直径，根据平角定义有\(\angle AOE = 180^{\circ}\) ，即\(\angle AOB + \angle BOE = 180^{\circ}\)。
因为\(\angle AOB\)与\(\angle COD\)互补（已知\(\angle AOB + \angle COD = 180^{\circ}\)），根据等量代换可得\(\angle BOE = \angle COD\) 。
弦长关系推导
在同圆中，相等圆心角所对弦相等，由于\(\angle BOE = \angle COD\)，所以\(BE = CD = 6\) （已知\(CD = 6\)）。
利用勾股定理求\(AB\)长
\(AE\)是直径，半径为\(5\)，则\(AE = 2\times5 = 10\)；又因为直径所对圆周角为直角，所以\(\angle ABE = 90^{\circ}\) 。
根据勾股定理\(AB = \sqrt{AE^{2} - BE^{2}}\)，代入\(AE = 10\)、\(BE = 6\)，可得：
\(AB = \sqrt{10^{2} - 6^{2}} = \sqrt{100 - 36} = \sqrt{64} = 8\) 。
答案：
弦 AB 的长为 8，故本题的答案是 B 选项。